A floating-point (FP) number is a kind of fraction where the radix point is allowed to move. If the radix point is fixed, then those fractional numbers are called fixed-point numbers. The best example of fixed-point numbers are those represented in commerce, finance while that of floating-point is the scientific constants and values.

The disadvantage of fixed-point is that not all numbers are easily representable. For example, continuous fractions are difficult to be represented in fixed-point form. Also, very small and very large fractions are almost impossible to be fitted with efficiency.
A floating-point number representation is standardized by IEEE with three components namely the sign bit, Mantissa and the exponent. The number is derived as:
F = (-1)s M x 2E
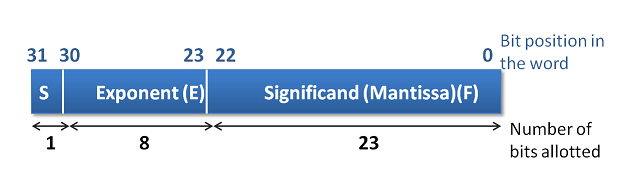
IEEE-754 standard prescribes single precision and double precision representation as in figure 10.1.

Floating point normalization
The mantissa part is adjusted in such a way that the value always starts with a leading binary '1' i.e. it starts with a non zero number. This form is called a normalized form. In doing so, the '1' is assumed to be the default and not stored and hence the mantissa 23 or 52 bits get extra space for representing the value. However, during calculations, the '1' is brought in by the hardware.
Floating point operations and hardware
Programming languages allow data type declaration called real to represent FP numbers. Thus it is a conscious choice by the programmer to use FP. When declared real the computations associated with such variables utilize FP hardware with FP instructions.
Add Float, Sub Float, Multiply Float and Divide Float is the likely FP instructions that are associated and used by the compiler. FP arithmetic operations are not only more complicated than the fixed-point operations but also require special hardware and take more execution time. For this reason, the programmer is advised to use real declaration judiciously. Table 10.1 suggests how the FP arithmetic is done.
| Addition | X+Y | (adjusted Xm + Ym) 2Ye where Xe ≤ Ye |
| Subtraction | X-Y | (adjusted Xm - Ym) 2Ye where Xe ≤ Ye |
| Multiplication | X x Y | (adjusted Xm x Ym) 2Xe+Ye |
| Division | X/Y | (adjusted Xm / Ym) 2Xe-Ye |
Addition and Subtraction
FP addition and subtraction are similar and use the same hardware and hence we discuss them together. Let us say, the X and Y are to be added.
Algorithm for FP Addition/Subtraction
Let X and Y be the FP numbers involved in addition/subtraction, where Ye > Xe.
Basic steps:
- Compute Ye - Xe, a fixed point subtraction
- Shift the mantissa of Xm by (Ye - Xe) steps to the right to form Xm2Ye-Xe if Xe is smaller than Ye else the mantissa of Ym will have to be adjusted.
- Compute Xm2Ye-Xe ± Ym
- Determine the sign of the result
- Normalize the resulting value, if necessary
We explain this with an example and as below:

Subtraction is done the same way as an addition.
Multiplication and Division
Multiplication and division are simple because the mantissa and exponents can be processed independently. FP multiplication requires fixed point multiplication of mantissa and fixed-point addition of exponents. As discussed in chapter 3 (Data representation) the exponents are stored in the biased form. The bias is +127 for IEEE single precision and +1023 for double precision. During multiplication, when both the exponents are added it results in excess 127. Hence the bias is to be adjusted by subtracting 127 or 1023 from the resulting exponent.

Floating Point division requires fixed-point division of mantissa and fixed point subtraction of exponents. The bias adjustment is done by adding +127 to the resulting mantissa. Normalization of the result is necessary in both the cases of multiplication and division. Thus FP division and subtraction are not much complicated to implement.
All the examples are in base10 (decimal) to enhance the understanding. Doing in binary is similar.
Floating Point Hardware
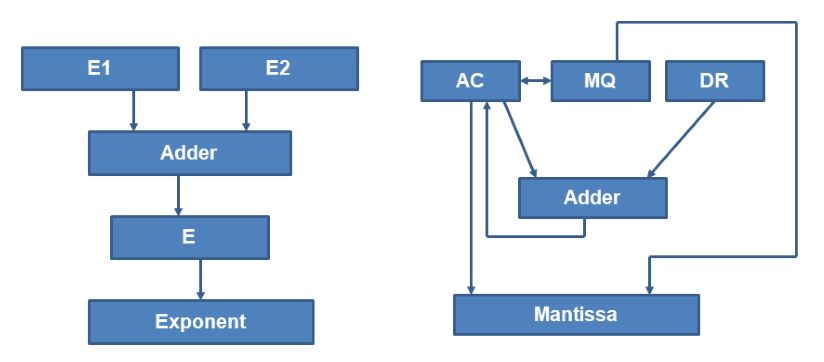
The floating-point arithmetic unit is implemented by two loosely coupled fixed point datapath units, one for the exponent and the other for the mantissa. One such basic implementation is shown in figure 10.2.
Along with early CPUs, Coprocessors were used for doing FP arithmetic as FP arithmetic takes at least 4 times more time than the fixed point arithmetic operation. These coprocessors are VLSI CPUs and are closely coupled with the main CPU. 8086 processor had 8087 as coprocessor; 80x86 processors had 80x87 as coprocessors and 68xx0 had 68881 as a coprocessor. Pipelined implementation is another method to speed up the FP operations. Pipelining has functional units which can do the part of the execution independently.
Additional issues to be handled in FP arithmetic are:
- FP arithmetic results will have to be produced in normalised form.
- Adjusting the bias of the resulting exponent is required. Biased representation of exponent causes a problem when the exponents are added in a multiplication or subtracted in the case of division, resulting in a double biased or wrongly biased exponent. This must be corrected. This is an extra step to be taken care of by FP arithmetic hardware.
- When the result is zero, the resulting mantissa has an all zero but not the exponent. A special step is needed to make the exponent bits zero.
- Overflow – is to be detected when the result is too large to be represented in the FP format.
- Underflow – is to be detected when the result is too small to be represented in the FP format. Overflow and underflow are automatically detected by hardware, however, sometimes the mantissa in such occurrence may remain in denormalised form.
- Handling the guard bit (which are extra bits) becomes an issue when the result is to be rounded rather than truncated.

