In a simple approach, Division is a successive subtraction. An arithmetic division is more complex than multiplication in the sense that a divide instruction requires more time to get executed. A Binary division is much simpler than decimal division because the quotient digits are either 0 or 1 and there is no need to estimate how many times the dividend or partial remainder fits into the divisor. The objective of a division is to divide the Dividend by the Divisor and obtain the Quotient and Remainder. Let us see the example of dividing 213 with 5 in binary form. The workout as below.
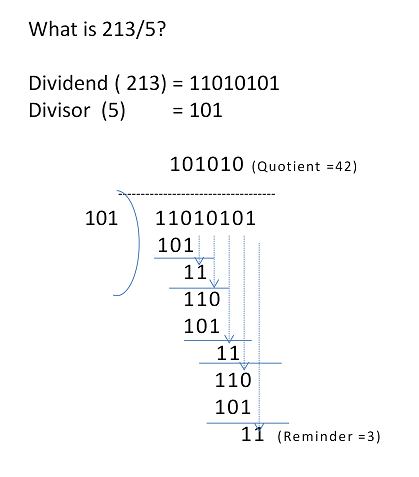
On dividing, we obtained 42 as quotient and 3 as remainder. Observe that:
- The number of bits taken at the first instance equals that of the bits in the divisor; these bits are considered from MSB onwards. In this case, it is 3-bits at a time.
- This set of bits from the dividend are compared with divisor. If dividend set is greater than the divisor, a '1' is placed in the quotient, else a '0' is placed in quotient.
- The partial reminder at this stage is derived by subtraction of the divisor from the dividend set of bits.
- The next most significant bit from the divisor is appended to the partial reminder.
- The divisor is shifted right.
- Steps 2 to 5 are repeated until all the bits in dividend are used up
In the hardware implementation of division the dividend or partial remainder is shifted to the left than shifting the divisor to the right. Thus, the two numbers are left in the required relative position. Subtraction is achieved by adding it's 2's complement of the divisor to the dividend. The information about the relative magnitudes i.e. whether the dividend set is greater than divisor is available from the end-carry.
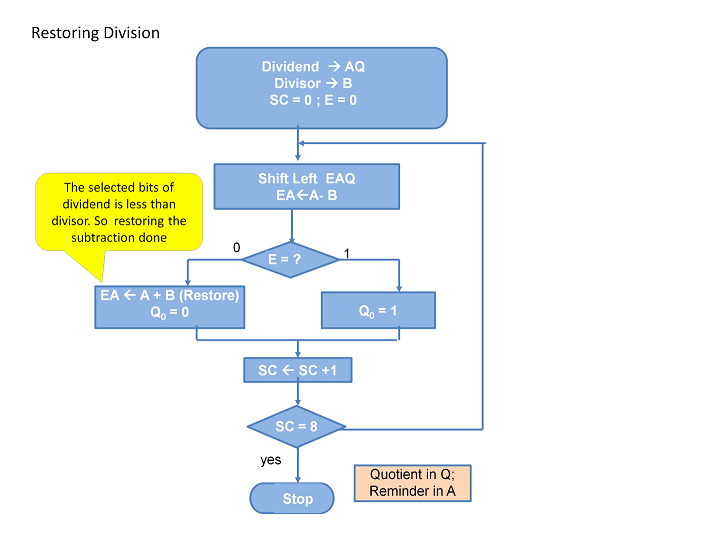
Restoring Division
In the process of division, at each step, we need to know whether the dividend set is higher than the divisor. This can be done by subtraction or comparison. Restoring division is a method wherein, by default, without identifying the magnitude of the dividend set, the divisor is subtracted. This is called trial subtraction. If the result of trial subtraction is positive, then the quotient is marked '1' and also the subtraction becomes the desired step. However, if the trial subtraction result is negative then this becomes an undesired step necessitating a correction; and hence the step is reverted or restored by adding the divisor. Subsequently, the quotient is marked '0. For this reason, this method of division algorithm is called Restoring Division method.
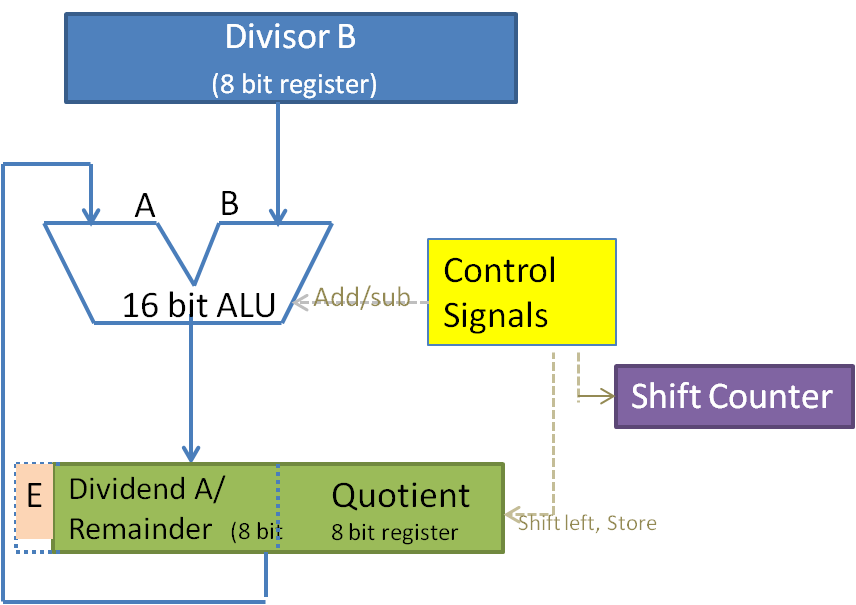
The datapath for the division is quite similar to that of multiplication but for the control signals and is as shown in figure 9b.1. The divisor, the dividend, the quotient are all n-bit registers. The dividend is extended with one bit 'E' for evaluating relative magnitude. E-bit and Registers A and Q are considered together as EAQ register. As shift left happens, the dividend set becomes available in A and quotient gets collected into Q. The shift counter keeps track of the number of bits in Dividend which is generally equal to the word size. The operation is repeated until all the bits of the dividend are evaluated.
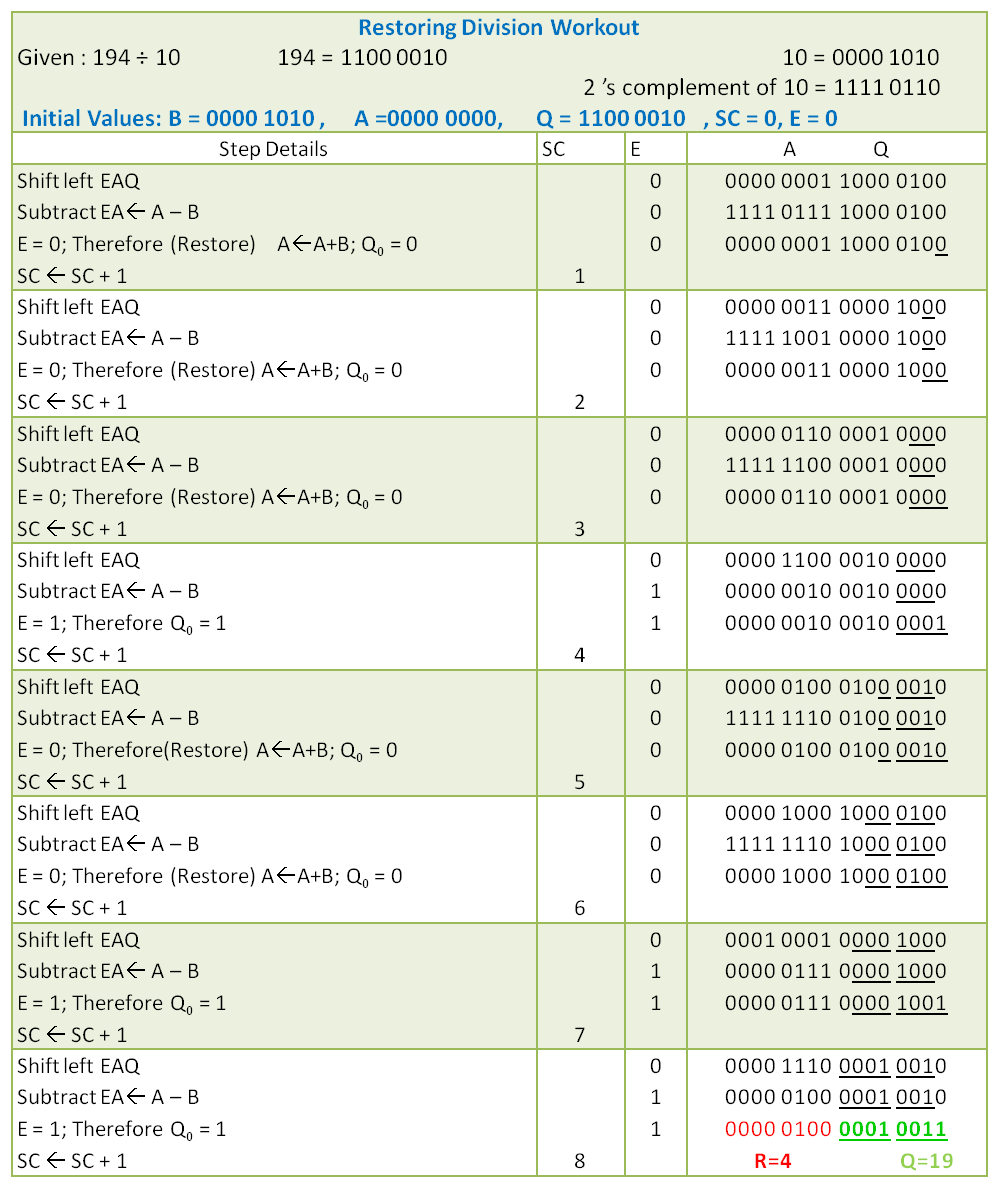
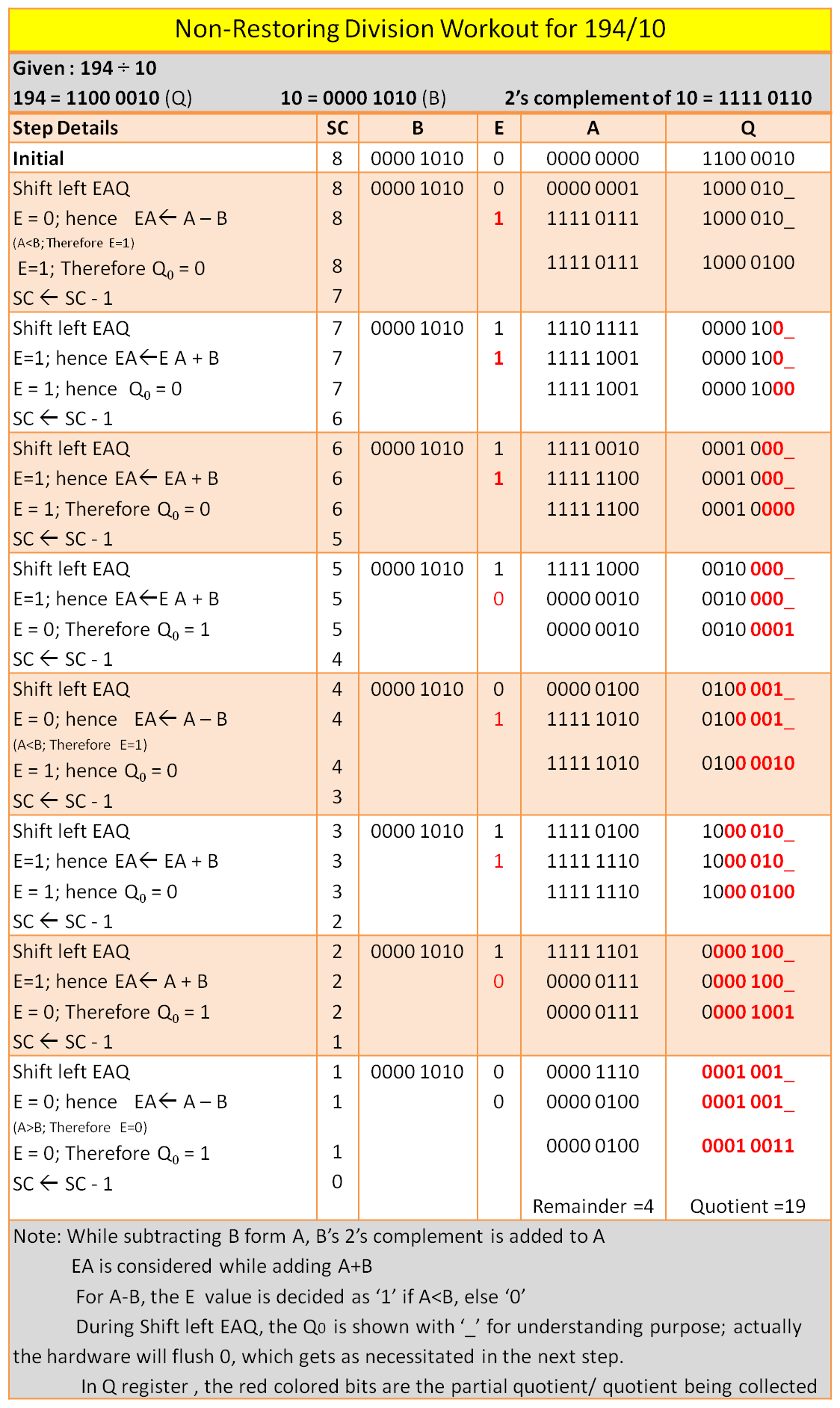
The flowchart in figure 9b.2 clearly explains the algorithmic process. Table 9b.1 demonstrates the workout for the division of 194รท10. From the work out we can understand the high volume of operations required to complete an 8-bit division. We have looped 8 times. It can be generally said that 50% of the cases restoring addition is required increasing the time overhead.
This method deals the dividend and divisor as unsigned numbers. The sign is adjusted after the division is done. The sign of the quotient is determined from the signs of the Divisor and the Dividend. The sign of the remainder is the same as that of the Dividend.
Non-Restoring Division
The non-restoring division is expected to eliminate the 50% overhead due to restoration.
In restoring algorithm on finding A-B to be negative, restoration was done by adding B. we have (A-B+B = A) then left shift was done (we have 2A). In the subsequent iteration, A-B will be found out. (making it 2A-B).
In the non-restoring algorithm, on finding A-B to be negative, B is not added right then. Instead, it proceeds with shift left (making it 2(A-B) ). In the next time around the loop B is added (making it 2A-2B+B=2A-B). The correction is applied at the stage of the final remainder as in flowchart 9b.3. The datapath is identical as in figure 9b.1.
Thus the result of the division is the same with increased efficiency. The same 194รท10 is used in the worksheet.
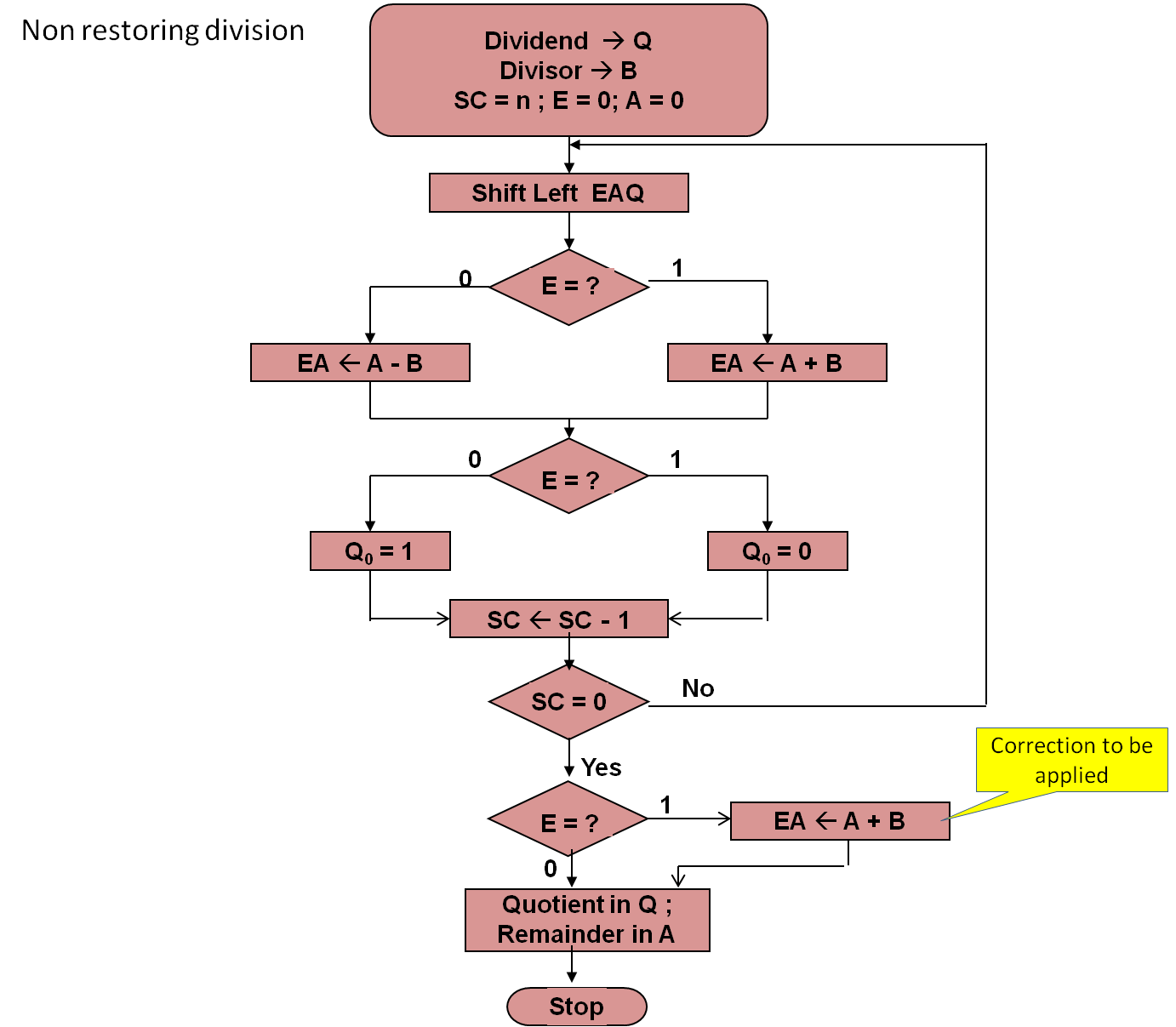
Basic steps of non-restoring division:
- Initialise E and A to zero. Load Dividend in Q, divisor in B. Load shift register with word size (n) value.
- Shift Left EAQ by 1.
- If E value is '0' find A-B else find A+B
- If the new E value is '0' set Quotient to '1' else '0'
- Reduce shift counter by '1'
- Repeat steps 2 to 5 until the shift counter > 0
- Correction is required for the final remainder if E value is '1' i.e. A is negative. Do the correction using A = A+B
- The final remainder in A register. Final Quotient in Q register.
Divide Overflow
An overflow is a situation that the resulting number is not larger than that can be represented in a word. Thus divide overflow occurs when the divisor value is 0' i.e any dividend being divided by zero results in Divide Overflow. It can also happen if the resulting quotient is too large to be fit into the variable defined in the program. Divide overflow generates an exception in the hardware.

